AVL 트리와 마찬가지로 자가 균형 트리의 종류
모든 노드는 레드 혹은 블랙으로 표현되며 이 색깔의 성질에 의해 트리의 균형이 맞춰진다. 균형이 완벽하지는 않지만 여전히 트리의 높이가 O(logN)에 보장되며 이는 탐색, 삽입, 삭제를 O(logN)에 보장하게 된다.
레드 블랙 트리의 성질
- 모든 노드는 레드 혹은 블랙이다.
- 루트 노드는 항상 검정이다.
- 레드 노드의 자식노드는 항상 검정이다.
- 한 노드에서 리프 노드까지 가는 모든 경로상에 만나는 검정 노드의 수는 모든 경로가 같은 수를 가져야 한다.
- Null 자식 노드는 검정 노드이다.
레드 블랙트리의 정의에 따라 한 노드에서 자기 자신을 제외한 리프 노드까지 도달하는데 만나는 블랙 노드의 수를 black height라고 하고 bh(v)라고 표현할 수 있다.
모든 레드 블랙트리의 높이는 O(logN)이다.
증명은 다음과 같이 가능하다.
가정 : v의 서브트리의 내부 노드 갯수 (NULL 노드를 제외한 모든 노드 수) $>= 2^{bh(v)} -1$ 를 만족한다.
기저 케이스 : v가 Null 노드 일 경우 $0 >= 2^0 -1 = 0$
귀납적 유도:

height(root) = h, height(left) = h-1, height(right) = h-1 이라 하면,
각 노드의 서브트리의 내부 노드 갯수는 다음을 만족 한다.
$ S(w) >= 2^{bh(w)} -1 $
$ S(z) >= 2^{bh(z)} -1 $
$ S(v) = S(w) + S(z) + 1 >= 2^{bh(w)} + 2^{bh(z)} - 1 $
블랙 노드의 자식 노드는 레드 혹은 블랙이므로
$bh(w), bh(z) >= bh(v) -1$
$ S(v) >= 2^{bh(w)} + 2^{bh(z)} - 1 = 2^{bh(v)} - 1$
4번 성질에 의하여 한 노드에서 리프노드 경로 상의 블랙 노드 수는 높이의 반보다는 크다.
$bh(v) >= h/2$
따라서,
$ n >= S(v) >= 2^{bh(v)} - 1 = 2^{h/2}-1 $ 이므로
$ h <= 2log_2{(n+1)} = O(log_2 n) $을 만족한다.
N개의 노드를 갖는 레드 블랙트리의 높이는 O(logN)이다.
레드블랙트리 삽입
로직은 다음과 같다.
1. BST의 일반적인 노드 삽입을 한다.
2. 삽입한 노드는 무조건 red로 생각한다.
3. 삽입한 노드를 x라하면, 다음 4가지 경우로 나뉜다.
(1) x == root 인 경우, x의 색깔을 black으로 바꾼다. (루트는 블랙)
(2) x의 parent의 색깔이 black이면 아무것도 하지 않는다.
(3) x의 parent가 red일 경우 다음 두가지로 나뉜다.
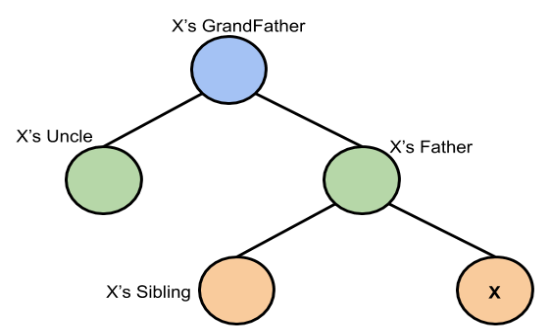
(3-1) x의 uncle(같은 조부모를 가지는 부모의 형제 노드)이 red인 경우, parent와 uncle은 모두 red이므로 parent와 uncle을 black으로 칠하고 grandparent부터 x로 생각하고 3번을 다시 검사한다.
(3-2) uncle이 black이라면 다음 4가지 경우로 나뉜다.
- Left-Right / Left-Left / Right-Left / Right-Right
자세한 트리 구조는 여기서 참고한다.
www.geeksforgeeks.org/red-black-tree-set-2-insert/
Red-Black Tree | Set 2 (Insert) - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
그 중 하나를 보면 Left-Left 경우
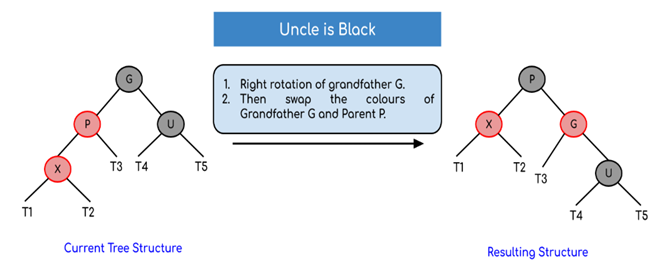
parent와 노드 x는 grandparent를 기준으로 왼쪽에 있으며 RightRotate(G)와 SwapColor(G,P) 연산을 해준다.
레드블랙트리 삭제
더블 블랙
삭제되는 노드를 v, 대체되는 노드를 u라할 때, u와 v가 모두 블랙 인 경우 더블 블랙이라하며 블랙 높이를 맞추기 위해 트리를 재구성한다.
로직은 다음과 같다.
1. BST의 일반적인 노드 삭제를 한다. (삭제되는 노드 v의 색깔을 기억하고 있어야한다.)
2. u와 v, 둘 중 하나가 red라면 삽입하는 노드 u를 black으로 칠한다.
3. u와 v가 모두 black, u가 double black 이라면, single black으로 바꾸는 작업을 한다.
- u가 double black이고 루트가 아닐때, u의 형제 노드(sibling)를 s라하자.
(a) s가 black이고 s의 자식 중 하나라도 red가 있는 경우 s에 대한 회전을 수행한다. s의 자식 중 red인 것을 r이라 하면, p를 기준으로 또다시 s와 r의 위치에 따라 다음 4가지 경우로 나뉜다.
- Left-Left / Left-Right / Right-Right / Right-Left
www.geeksforgeeks.org/red-black-tree-set-3-delete-2/?ref=lbp
Red-Black Tree | Set 3 (Delete) - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
(b) s가 black이고 s의 모든 자식이 black이라면, s를 red로 칠하고 다음 두 경우를 생각한다.
(b-1) s의 부모 p가 red이라면 p를 black으로 칠한다.
(b-2) p가 black이라면 p에 대한 double black를 검사한다. doubleblack(p, vcolor:=black);
(c) s가 red라면, parent와 sibling의 색을 반전시킨다. 다음 두 경우로 나뉜다.
(c-1) s가 parent 기준으로 왼쪽이면 RightRotate(P)
(c-2) s가 parent 기준으로 오른쪽이라면 LeftRotate(P)를 수행한다.

구현 코드
삽입은 제대로 되지만 삭제는 보완이 필요하다...
#pragma once
#include <iostream>
#include <cassert>
#include <cstdlib>
#include <stack>
enum class Color
{
Red = 0,
Black = 1,
};
template<typename T>
class RBTNode
{
template<typename T>
friend class RedBlackTree;
private:
public:
T _val;
Color _color;
RBTNode<T>* _parent = nullptr;
RBTNode<T>* _left = nullptr;
RBTNode<T>* _right = nullptr;
private:
RBTNode(T val, Color color)
:
_val(val),
_color(color)
{
}
};
template<typename T>
class RedBlackTree
{
private:
using Node = RBTNode<T>;
using NodePtr = RBTNode<T>*;
private:
NodePtr _root = nullptr;
public:
RedBlackTree() {}
~RedBlackTree()
{
Clear();
}
void Clear()
{
std::stack<NodePtr> stk;
NodePtr cur = _root, nxt;
while (cur != nullptr || !stk.empty())
{
// reach left-most node of curr node
while (cur != nullptr)
{
stk.push(cur);
cur = cur->_left;
}
// pop from top of stack (leftmost)
cur = stk.top();
stk.pop();
nxt = cur->_right;
delete cur;
cur = nxt;
}
_root = nullptr;
}
void Insert(T val)
{
if (!_root)
{
_root = new Node(val, Color::Black);
return;
}
Insert(_root, val);
}
void Erase(T val)
{
if (!_root)
return;
_root = Erase(_root, val);
}
void Print() const
{
std::cout << "================ Tree Node ===============" << std::endl;
Print(_root);
std::cout << std::endl;
}
private:
bool IsRed(NodePtr const& node)
{
if (!node) return false;
return node->_color == Color::Red;
}
void SwapColor(NodePtr const& NodeA, NodePtr const& NodeB)
{
Color colorB = NodeB ? NodeB->_color : Color::Black;
if (NodeB)
NodeB->_color = NodeA ? NodeA->_color : Color::Black;
if (NodeA)
NodeA->_color = colorB;
}
NodePtr RightRotate(NodePtr const& node)
{
NodePtr leftRight = node->_left->_right;
// 왼쪽 자식 재조정
node->_left->_parent = node->_parent;
node->_left->_right = node;
// 부모 재조정
if (node->_parent)
{
bool IsLeftChild = node->_parent->_left == node;
if (IsLeftChild)
node->_parent->_left = node->_left;
else
node->_parent->_right = node->_left;
}
node->_parent = node->_left;
node->_left = leftRight;
// 왼쪽 자식의 오른쪽 노드
if(leftRight)
leftRight->_parent = node;
// 루트 일 경우 재조정
if (node == _root)
_root = node->_parent;
return node->_parent;
}
NodePtr LeftRotate(NodePtr const& node)
{
NodePtr rightLeft = node->_right->_left;
// 오른쪽 자식 재조정
node->_right->_parent = node->_parent;
node->_right->_left = node;
// 부모 재조정
if (node->_parent)
{
bool IsLeftChild = node->_parent->_left == node;
if (IsLeftChild)
node->_parent->_left = node->_right;
else
node->_parent->_right = node->_right;
}
node->_parent = node->_right;
node->_right = rightLeft;
// 오른쪽 자식의 왼쪽 노드
if (rightLeft)
rightLeft->_parent = node;
// 루트 일 경우 재조정
if (node == _root)
_root = node->_parent;
return node->_parent;
}
NodePtr RRrotation(NodePtr gf, NodePtr f)
{
NodePtr root = LeftRotate(gf);
SwapColor(gf, f);
return root;
}
NodePtr LLrotation(NodePtr gf, NodePtr f)
{
NodePtr root = RightRotate(gf);
SwapColor(gf, f);
return root;
}
NodePtr FindMin(NodePtr const& node)
{
if (!node->_left)
return node;
return FindMin(node->_left);
}
private:
void Print(NodePtr const& node) const
{
if (!node) return;
Print(node->_left);
std::cout << node->_val << (node->_color == Color::Red ? "[R] " : "[B] ");
Print(node->_right);
}
void InsertCheck(NodePtr parent, NodePtr const& insertedNode)
{
if (!parent)
return;
// 부모가 블랙이라면 확인할 필요 없음
if (parent->_color == Color::Black)
return;
NodePtr GrandParent = parent->_parent;
NodePtr Uncle = GrandParent->_right == parent ? GrandParent->_left : GrandParent->_right;
// 삼촌도 레드
if (Uncle && Uncle->_color == Color::Red)
{
Uncle->_color = Color::Black;
parent->_color = Color::Black;
// 조부모부터 다시 확인
InsertCheck(GrandParent->_parent, GrandParent);
}
// 삼촌은 블랙
else
{
if (parent->_right == insertedNode)
{
// Right-Right
if (GrandParent->_right == parent)
{
RRrotation(GrandParent, parent);
}
// Left-Right
else
{
parent = LeftRotate(parent);
// LL
LLrotation(GrandParent, parent);
}
}
else
{
// Left-Left
if (GrandParent->_left == parent)
{
LLrotation(GrandParent, parent);
}
// Right-Left
else
{
parent = RightRotate(parent);
// RR
RRrotation(GrandParent, parent);
}
}
}
}
void Insert(NodePtr const &node, const T& val)
{
if (node->_val < val)
{
if (node->_right)
{
return Insert(node->_right, val);
}
node->_right = new Node(val, Color::Red);
node->_right->_parent = node;
InsertCheck(node, node->_right);
}
else if (node->_val > val)
{
if (node->_left)
{
return Insert(node->_left, val);
}
node->_left = new Node(val, Color::Red);
node->_left->_parent = node;
InsertCheck(node, node->_left);
}
}
void FixTree(NodePtr u, Color vColor)
{
if (u == _root)
{
u->_color = Color::Black;
return;
}
// 1. Simple Case : Either u or v is red
bool uIsRed = IsRed(u);
bool vIsRed = vColor == Color::Red;
if (uIsRed || vIsRed)
{
u->_color = Color::Red;
}
// 2. both u and v are black (double black) and u is not root, it is complicated
else if (!uIsRed && !vIsRed && u != _root)
{
NodePtr parent = u->_parent;
bool siblingIsRight = parent->_left == u;
NodePtr sibling = siblingIsRight ? parent->_right : parent->_left;
// 2. (a) sibiling color is black
if (sibling->_color == Color::Black)
{
// all children are black
if (!IsRed(sibling->_right) && !IsRed(sibling->_left))
{
// recoluring
sibling->_color = Color::Red;
// if parent color is black, recur for parent
if (parent->_color == Color::Black)
FixTree(parent, Color::Black);
else
parent->_color = Color::Black;
return;
}
// at least one of children is red
if (siblingIsRight)
{
// RR case
if (IsRed(sibling->_right))
{
sibling->_right->_color = sibling->_color;
sibling->_color = parent->_color;
parent = LeftRotate(parent);
}
// RL case
else if(IsRed(sibling->_left))
{
sibling->_left->_color = parent->_color;
RightRotate(sibling);
parent = LeftRotate(parent);
}
}
else
{
// LL case
if (IsRed(sibling->_left))
{
sibling->_left->_color = sibling->_color;
sibling->_color = parent->_color;
parent = RightRotate(parent);
}
// LR case
else if (IsRed(sibling->_right))
{
sibling->_right->_color = parent->_color;
LeftRotate(sibling);
parent = RightRotate(parent);
}
}
}
// 2. (b) sibiling color is red
else
{
bool siblingIsRight = parent->_left == u;
parent->_color = Color::Red;
sibling->_color = Color::Black;
if (siblingIsRight)
{
LeftRotate(parent);
}
else
{
RightRotate(parent);
}
// recur for u
FixTree(u, Color::Black);
}
}
}
NodePtr Erase(NodePtr node, const T& val)
{
if (node->_val == val)
{
// 리프 노드이거나 왼쪽에만 서브트리가 존재
if(!node->_right)
{
NodePtr leftTree = node->_left;
if (node->_parent)
node->_parent->_right = leftTree;
if (leftTree)
leftTree->_parent = node->_parent;
delete node;
return leftTree;
}
NodePtr rightMin = FindMin(node->_right);
node->_val = rightMin->_val;
Color vColor = node->_right->_color; // temporary storation
NodePtr rightNext = Erase(node->_right, rightMin->_val);
bool needFix = node->_right != rightNext; // changes by deletion
node->_right = rightNext;
if (needFix)
{
FixTree(node->_right, vColor);
}
}
else if (node->_left && val < node->_val)
{
node->_left = Erase(node->_left, val);
}
else if (node->_right && val > node->_val)
{
node->_right = Erase(node->_right, val);
}
return node;
}
};#include "RedBlackTree.h"
#include <iostream>
#include <cstdlib>
#include <vector>
#include <functional>
#include <algorithm>
#include <crtdbg.h>
using namespace std;
int main()
{
_CrtDumpMemoryLeaks();
srand((unsigned int)time(NULL));
// 삽입 테스트
for (int test = 0; test < 10; ++test)
{
RedBlackTree<int> tree;
// 1~100 숫자 셔플해서 트리에 삽입
vector<int> element;
for (int i = 1; i <= 100; ++i)
{
element.push_back(i);
}
random_shuffle(element.begin(), element.end());
for (int& v : element)
{
tree.Insert(v);
}
tree.Print();
tree.Clear();
}
// 삭제 테스트
RedBlackTree<int> tree;
vector<int> element;
for (int i = 1; i <= 10; ++i)
{
element.push_back(i);
}
random_shuffle(element.begin(), element.end());
for (int& v : element)
{
tree.Insert(v);
}
random_shuffle(element.begin(), element.end());
for (int& v : element)
{
tree.Erase(v);
tree.Print();
}
return 0;
}

'C++ > 자료 구조' 카테고리의 다른 글
| [자료 구조] 원형 버퍼 CircularBuffer (0) | 2021.08.23 |
|---|---|
| [자료구조] 알아야 할 자료구조 B-Tree (1) | 2021.05.11 |
| [자료구조] 알아야 할 자료구조 Heap (0) | 2021.04.16 |
| [자료 구조] 알아야 할 자료구조 AVL Tree (0) | 2021.03.31 |
| [자료 구조] 알아야 할 자료구조 Binary Search Tree (0) | 2021.03.31 |