C++/자료 구조

[자료 구조] 알아야 할 자료구조 AVL Tree

로파이 2021. 3. 31. 17:37

AVL (Adelson-Velsky and Landis) Tree

이진 자가 균형 트리

 

- 균형 트리

이진 탐색 트리의 경우 삽입이나 삭제 이후 서브 트리간 불균형 문제가 발생할 수 있다. 이는 추후 탐색 시간을 저하시키기 때문에 균형을 맞추는 것이 필요하다.

 

- 높이의 정의

한 노드의 높이는 노드를 루트로하는 서브 트리에서 말단 리프노드까지 도달하는 경로 중 가장 긴 경로를 의미한다.

재귀적 표현으로 높이를 구한다면 다음과 같다. 

 

height := max(height(left_child), height(right_child)) + 1

 

위 계산을 편리하게 하기위해 Null 노드의 높이를 -1로 설정한다.

 

height = -1 if (root == NULL)

 

- AVL Tree의 구조

AVL tree

AVL tree는 스스로 균형을 맞추는 트리로 왼쪽 서브 트리와 오른쪽 서브 트리의 높이차가 1보다 크지 않은 트리를 의미한다.

높이 h를 가지는 AVL 트리의 노드 개수를 $N_h$라하면, 

$N_h = 1 + N_{h-1} + N_{h-2}$

를 만족한다. $N_h$는 다음과 같이 쓸 수 있으므로

$N_h = 1 + N_{h-1} + N_{h-2}$

$> 1 + 2N_{h-2}$

$> 2N_{h-2}$

$      = \Theta(2^{h/2})$

$h < 2logN_h = O(logN)$

즉, 트리의 높이는 항상 전체 노드 갯수의 log 값보다 작으므로 탐색은 최악의 경우 $O(h = logN)$을 보장한다.

 

- AVL 노드 구조

template <typename Key>
class AVLTreeNode
{
	template<typename Key>
	friend class AVLTree;
public:
	int _height = 0;
	Key _key;
	AVLTreeNode* _left = nullptr;
	AVLTreeNode* _right = nullptr;
private:
	AVLTreeNode(Key key)
		: _key(key)
	{
	}
	~AVLTreeNode()
	{
		delete _left;
		delete _right;
	}
};

기본 BST 노드와 동일하며 매번 노드의 height를 계산하지 않고 따로 height를 계산하여 저장해놓는다. 

 

height 관련 utility function

// utility functions
int height(NodePtr root)
{
  if (!root)
    return -1;
    return root->_height;
}
int factor(NodePtr root)
{
	return height(root->_left) - height(root->_right);
}

- 불균형 노드

어떤 노드가 불균형하다는 의미는 두 서브 트리의 높이 차가 1보다 큰 경우를 의미한다. 높이 차를 balance factor라고 하며 이를 해결하기위해 한 노드에 대해 다음 두 회전 연산을 수행할 수 있다.

 

출처: https://www.geeksforgeeks.org/avl-tree-set-1-insertion/

LeftRotation 왼쪽 회전(y) RightRotation 오른쪽 회전(x)
y의 왼쪽에는 T2가 위치한다.
x의 오른쪽에는 y가 위치한다.		 x의 오른쪽에는 T2가 위치한다.
y의 왼쪽에는 x가 위치한다.

두 회전 연산 이후 T1, T2, T3의 높이는 변하지 않으며 x, y 에대한 높이를 계산하여 업데이트 한다.

// x, y 에 대한 height 업데이트
x->_height = max(height(x->_left), height(x->_right)) + 1;
y->_height = max(height(y->_left), height(y->_right)) + 1;

AVL 트리 역시 이진 트리 성질을 만족해야하기 때문에 두 연산에 대한 결과는 이진 트리 성질을 깨지 않는다.

중위 순회 결과

왼쪽 회전 전 : T1->x->T2->y->T3    / 왼쪽 회전 후 : T1->x->T2->y->T3  

오른쪽 회전 전 : T1->x->T2->y->T3   / 오른쪽 회전 후 : T1->x->T2->y->T3  

 

- 회전의 균형 기능

정확한 증명은 아니지만 개념적으로 회전은 다음과 같이 트리를 조정하여 불균형성을 제거한다.

왼쪽회전

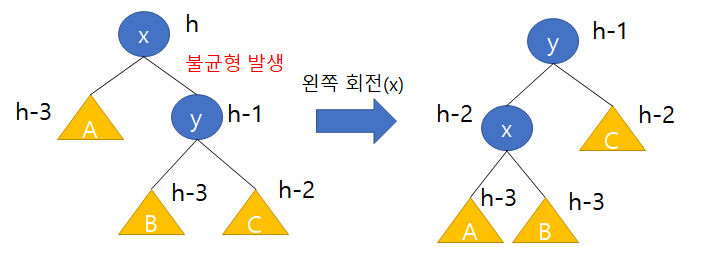
AVL트리의 삽입

AVL 트리의 노드 삽입은 일반적 BST의 삽입을 따른다. 삽입된 노드를 w이라하면 w를 포함하는 모든 서브 트리의 높이가 바뀌었는지 체크할 필요가 있다. w를 포함하는 모든 서브 트리의 루트는 w의 조상이 된다.

 

기본적인 원리는 삽입 이후부터 함수 재귀 종료 이전까지의 영역 backtracking을 통해 현재 root 노드가 불균형 한지 체크를 한후 그렇다면 balance를 수행한다. root가 재조정된다면 해당 재귀 함수 호출 종료 후 상위 호출을 통해 root의 root를 체크하고 결국 w에서 시작하여 모든 조상을 검사할 수 있다.

 

z를 w의 조상을 아래서 부터 차례대로 탐색하던 도중 첫번째 발견한 불균형 노드라하고 y를 w 노드에서 올라온 조상 중 z의 child, x를 w 노드에서 올라온 조상 중 y의 child라 하자.

 

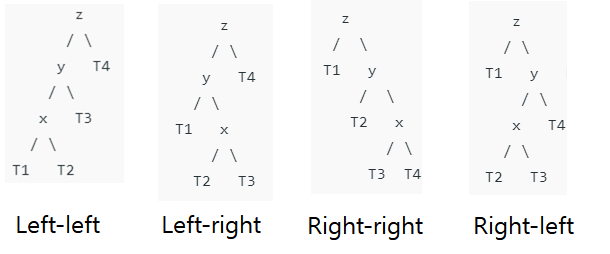
출처: https://www.geeksforgeeks.org/avl-tree-set-1-insertion/

그렇다면 z,y,x의 경우는 위 4가지 경우 이고 위 4가지에 대해 회전 연산으로 이루어진 4가지 해법을 적용 하면 된다. 

  • left-left : right rotate (z)
  • left-right : left rotate (y) -> right rotate (z)
  • right-right : left-rotate (z)
  • right-left : right-rotate (y) -> left rotate (z)

첫번째 위치는 y를 의미하고 두번째 위치는 x를 의미한다. y를 찾는 방법은 z의 balance factor를 조사하여 y를 결정하고 x는 y의 balance factor를 조사하여 0보다 크다면 왼쪽을 택하고 0보다 작거나 같으면 오른쪽을 택하면 된다. w가 삽입된 트리가 더 무겁기 때문이다.

 

- Rebalance 함수

NodePtr Rebalance(NodePtr z)
{
	int diff = factor(z);

	// Left case
	if (diff > 1)
	{
		bool leftCase = factor(z->_left) > 0;
		if (leftCase)
		{
			// Right Rotate (z)
			return rightRotate(z);
		}
		else
		{
			// Left Rotate (y) 
			z->_left = leftRotate(z->_left);
			// Right Rotate (z)
			return rightRotate(z);
		}
	}
	// Right case
	else if (diff < -1)
	{
		bool leftCase = factor(z->_right) > 0;
		if (leftCase)
		{
			// Left Rotate (y) 
			z->_right = rightRotate(z->_right);
			// Right Rotate(z)
			return leftRotate(z);
		}
		else 
		{
			return leftRotate(z);
		}
	}
	// no need to balance
	return z;
}

- 상위 루트로 탐색(삽입)

backtracking 영역에 적용되어 balance 이후 root의 높이를 재계산하고 root를 반환한다.

// 균형 잡기
root = Rebalance(root);

// root 높이 재 계산
root->_height = max(height(root->_left), height(root->_right)) + 1;

// 재귀 종료후 상위 루트로 탐색
return root;

 

AVL트리의 삭제

삭제의 경우도 비슷하다. 삭제 이후부터 함수 재귀 종료 이전까지의 영역 backtracking을 통해 현재 root 노드가 불균형 한지 체크를 한 후 그렇다면 balance를 수행한다. 

삽입과 똑같은 z,y,x 노드 토폴로지를 이용하며 첫번째로 균형이 무너진 z를 기준으로 z의 child 중 더 무거운 (높이가 큰) y를 선택하고 y의 child 중 더 무거운 x를 선택한다.

 

- 상위 루트로 탐색(삭제)

backtracking 영역에 적용되어 balance 이후 root의 높이를 재계산하고 root를 반환한다.

// 균형 잡기
root = Rebalance(root);

// 높이 업데이트
root->_height = max(height(root->_left), height(root->_right)) + 1;

// 정상 삭제 후 재귀 스택 호출 종료 
return root;

 

- 전체 코드

다음 중위 순회시 각 노드가 balance factor를 계산하여 불균형 노드가 있는지 검사한다. (디버깅)

int diff = factor(root);
bool balance = diff <= 1 && diff >= -1;
assert(balance);
더보기 
template <typename Key>
class AVLTree
{
public:
	using Node = AVLTreeNode<Key>;
	using NodePtr = AVLTreeNode<Key>*;
	~AVLTree()
	{
		delete _root;
	}
private:
	NodePtr _root = nullptr;
private:
	// utility functions
	int height(NodePtr root)
	{
		if (!root)
			return -1;
		return root->_height;
	}
	int factor(NodePtr root)
	{
		return height(root->_left) - height(root->_right);
	}
	/*
              y                               x
             / \     Right Rotation          /  \
	   x   T3   - - - - - - - >        T1   y
	  / \       < - - - - - - -            / \
	 T1  T2     Left Rotation            T2  T3
	*/
	NodePtr rightRotate(NodePtr const& y)
	{
		NodePtr x = y->_left;
		NodePtr T2 = x->_right;
		x->_right = y;
		y->_left = T2;

		// x, y 에 대한 height 업데이트
		x->_height = max(height(x->_left), height(x->_right)) + 1;
		y->_height = max(height(y->_left), height(y->_right)) + 1;

		// 새로운 루트
		return x;
	}
	NodePtr leftRotate(NodePtr const& x)
	{
		NodePtr y = x->_right;
		NodePtr T2 = y->_left;
		y->_left = x;
		x->_right = T2;

		// x, y 에 대한 height 업데이트
		x->_height = max(height(x->_left), height(x->_right)) + 1;
		y->_height = max(height(y->_left), height(y->_right)) + 1;

		// 새로운 루트
		return y;
	}
	NodePtr Rebalance(NodePtr z)
	{
		int diff = factor(z);

		// Left case
		if (diff > 1)
		{
			bool leftCase = factor(z->_left) > 0;
			if (leftCase)
			{
				// Right Rotate (z)
				return rightRotate(z);
			}
			else
			{
				// Left Rotate (y) 
				z->_left = leftRotate(z->_left);
				// Right Rotate (z)
				return rightRotate(z);
			}
		}
		// Right case
		else if (diff < -1)
		{
			bool leftCase = factor(z->_right) > 0;
			if (leftCase)
			{
				// Left Rotate (y) 
				z->_right = rightRotate(z->_right);
				// Right Rotate(z)
				return leftRotate(z);
			}
			else 
			{
				return leftRotate(z);
			}
		}
		// no need to balance
		return z;
	}
private:
	NodePtr Insert(Key key, NodePtr root)
	{
		// 삽입 시 부모 추가
		if (key < root->_key)
		{
			root->_left = root->_left ? Insert(key, root->_left) : new Node(key);
		}
		else if (key > root->_key)
		{
			root->_right = root->_right ? Insert(key, root->_right) : new Node(key);
		}

		// 균형 잡기
		root = Rebalance(root);

		// root 높이 재 계산
		root->_height = max(height(root->_left), height(root->_right)) + 1;

		// 재귀 종료후 상위 루트로 탐색
		return root;
	}
	NodePtr Search(Key key, NodePtr root)
	{
		// 키 찾았거나 없는 경우
		if (!root || key == root->_key)
			return root;

		if (key < root->_key)
			return Search(key, root->_left);
		else
			return Search(key, root->_right);
	}
	NodePtr Erase(Key key, NodePtr root)
	{
		// 키 찾지 못함
		if (!root)
			return root;

		if (key < root->_key)
		{
			root->_left = Erase(key, root->_left);
		}
		else if (key > root->_key)
		{
			root->_right = Erase(key, root->_right);
		}

		// 키를 찾은 경우
		if (key == root->_key)
		{
			// 리프 노드 혹은 왼쪽 서브 트리만 있는 노드에 도달한 경우 삭제하고 왼쪽 노드를 반환
			if (!root->_right)
			{
				NodePtr leftSubTree = root->_left;
				delete root;
				return leftSubTree;
			}

			// 오른쪽 서브트리에서 가장 작은 키를 가지는 노드를 찾는다.
			NodePtr rightSmallest = FindMinNode(root->_right);

			// 키 변경
			root->_key = rightSmallest->_key;

			// 재귀
			root->_right = Erase(rightSmallest->_key, root->_right);
		}

		// 균형 잡기
		root = Rebalance(root);

		// 높이 업데이트
		root->_height = max(height(root->_left), height(root->_right)) + 1;

		// 정상 삭제 후 재귀 스택 호출 종료 
		return root;
	}
	NodePtr FindMinNode(NodePtr root)
	{
		if (root->_left)
			return FindMinNode(root->_left);

		return root;
	}
	void InOrderTraversal(NodePtr root)
	{
		if (!root)
			return;

		int diff = factor(root);
		bool balance = diff <= 1 && diff >= -1;
		assert(balance);

		InOrderTraversal(root->_left);
		printf("%d ", root->_key);
		InOrderTraversal(root->_right);
	}
public:
	void Insert(Key key)
	{
		if (!_root)
		{
			_root = new Node(key);
			return;
		}
		_root = Insert(key, _root);
	}
	NodePtr Search(Key key)
	{
		return Search(key, _root);
	}
	void Erase(Key key)
	{
		_root = Erase(key, _root);
	}
	void Print()
	{
		InOrderTraversal(_root);
		printf("\n");
	}
};

 

- 정상 작동 체크

#include "Tree.h"
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main()
{
	srand((unsigned int)time(NULL));
	//BinarySearchTree<int> tree;
	AVLTree<int> tree;

	// 1~100 숫자 셔플해서 트리에 삽입
	vector<int> element;
	for (int i = 1; i <= 100; ++i)
	{
		element.push_back(i);
	}
	random_shuffle(element.begin(), element.end());

	for (int &v : element)
	{
		tree.Insert(v);
		cout << "AVL tree" << endl;
		tree.Print();
	}

	// 원소 제거
	for (int i = 1; i <= 100; ++i)
	{
		tree.Erase(i);
		cout << "After erase" << endl;
		tree.Print();
	}
    return 0;
}

'C++ > 자료 구조' 카테고리의 다른 글

[자료 구조] 원형 버퍼 CircularBuffer  (0) 2021.08.23
[자료구조] 알아야 할 자료구조 B-Tree  (0) 2021.05.11
[자료구조] 알아야 할 자료구조 Heap  (0) 2021.04.16
[자료구조] 알아야 할 자료구조 Red-Black Tree  (0) 2021.04.07
[자료 구조] 알아야 할 자료구조 Binary Search Tree  (0) 2021.03.31

'C++/자료 구조'의 다른글

  • 현재글[자료 구조] 알아야 할 자료구조 AVL Tree

관련글

티스토리툴바